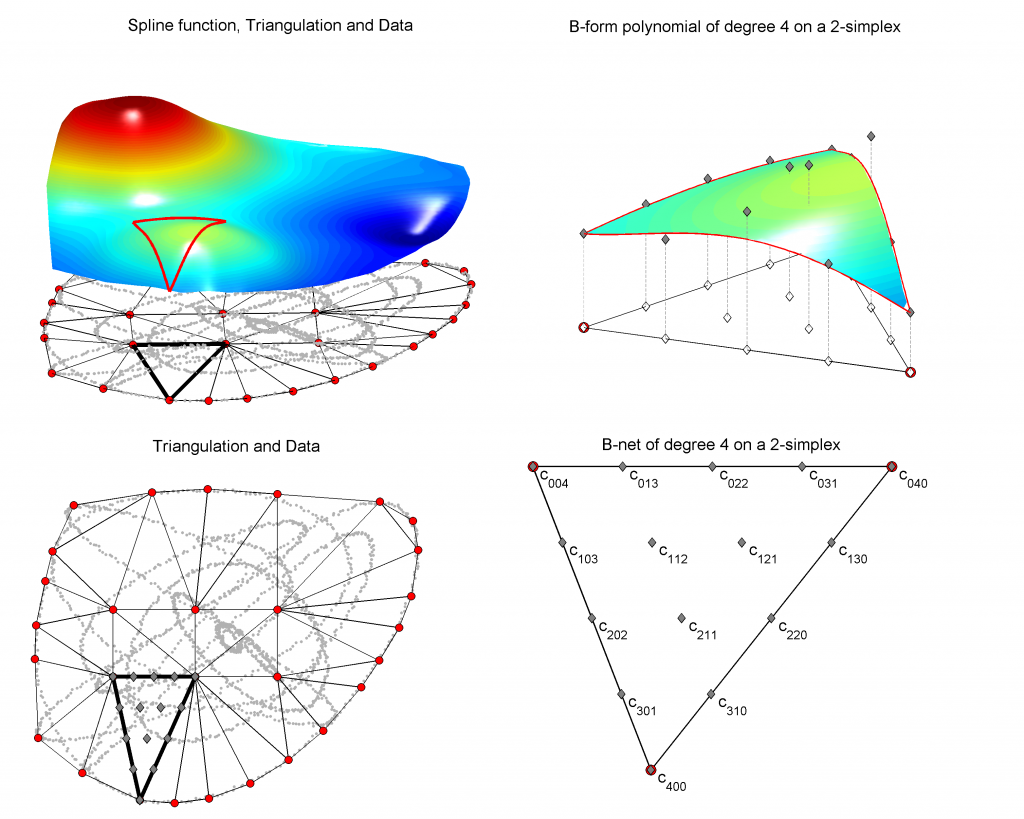
Multivariate B-splines are a powerful class of function approximators. Multivariate B-splines consist of local multivariate Bernstein basis polynomials defined on simplices. By smoothly combining any number of simplices, a function approximator with a very high approximation power can be created. The local basis functions of the multivariate splines are linear in the parameters, and standard linear regression methods such as least squares can be used to estimate these parameters (B-coefficients). Because of the local nature of the basis functions, the solution systems of the multivariate B-splines tend to be highly sparse, allowing the use of efficient (sparse) matrix solvers. The multivariate B-splines can be seen as a transparent and efficient alternative to the Neural Network class of function approximators.
Recent research performed at our group have led to the development of differential mapping operators that directly map a multivariate spline to any of its directional derivatives without loss of polynomial degree. With these mapping operators, the weak solution to PDEs can easily be calculated.
Current research in the multivariate B-spline focusses on:
- Differential mapping operators.
- PDE control using multivariate B-splines.
- Triangulation generalization and optimization.
- Physical basis transformations.
- Domain decomposition and fast distributed solvers.
The following video gives a demonstration of PDE control with multivariate splines: