Active Flow Control is a relatively recent field that combines the state of the art in applied and theoretical aerodynamics with that of control theory. Active Flow Control is considered a viable approach towards significantly reduced aerodynamic drag, improved noise characteristics, and improved lift characteristics of aircraft.
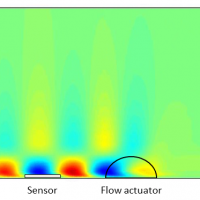
Active Flow Control combines some form of flow actuator, for example a plasma actuator, with flow sensors and a feedback control system. Developing such a control system is highly challenging however. The reason is that the flow system is completely determined by the well known Navier-Stokes equations, which constitutes an infinite dimensional system. While control of infinite dimensional systems is possible in theory, in practice such controllers are found to be fundamentally incompatible with physical actuation and sensing mechanisms.
The goal of this project is to develop a physically implementable feedback control system that combines physically implementable flow actuation and flow sensing.
Our approach uses multivariate B-splines to discretize the infinite dimensional system formed by the Navier-Stokes equations. The multivariate splines have a spectral-like approximation power and use smoothness and boundary conditions as side constraints. By projecting on the null-space of the constraint matrix, a Reduced Order Model (ROM) is created which also is a minimum realization of the original flow system. A unique result of our approach is that spline reduced order model (SROM) is of sufficiently low order (a few thousands of states in 2D) to allow the use of Balanced Truncation, which requires the calculation of the observability and controllability Gramians which becomes computationally intractable for systems of order 10000 and higher resulting from standard discretization (FEM) methods.
The final result is a low order state space model containing only a few tens of states for the 2D case. Based on this low order model, standard (linear) control theory can be used to design optimal (LQG, H2) or robust (Hinf) controllers. We can use linear control because it turns out that most controllable and observable flow characteristics are of linear nature, even in the turbulent flow regime.
Current research efforts are focussed on:
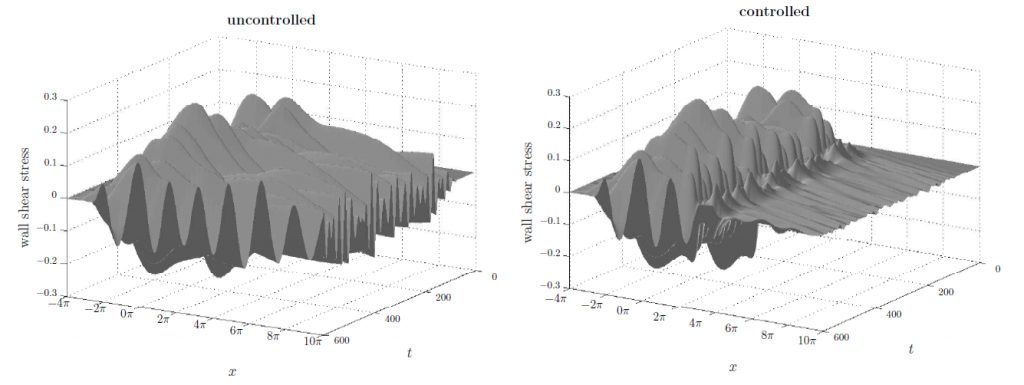
- Developing an H2 optimal controller for suppressing disturbances in flat plate boundary layer flows.
- Developing robust controllers that can cope with variations in the Reynolds number.
- Extending the approach to 3D flows.
- Developing a wind tunnel setup to test the new controllers.